用二次函数研究三次多项式函数的零点问题【中阶和高阶辅导】-白红宇

用二次函数研究三次多项式函数的零点问题【中阶和高阶辅导】

阅读量：6212 次

发布时间：2019-06-21

本文共 2234 字，大约阅读时间需要 7 分钟。

用二次函数研究三次多项式函数的零点问题，可以看成二次函数的又一个大作用。

设三次多项式函数$F(x)=ax^3+bx^2+cx+d(a>0)$，其导函数为二次函数$F'(x)=3ax^2+2bx+c$，导函数的判别式标记为$\Delta$，

1、若$\Delta\leq 0$，则$F'(x)\ge0$恒成立，所以$F(x)$在$R$上单调递增，有一个零点；

引申：若$\Delta > 0$，则$F'(x)\ge0$不恒成立，所以$F(x)$在$R$上不是单调递增。

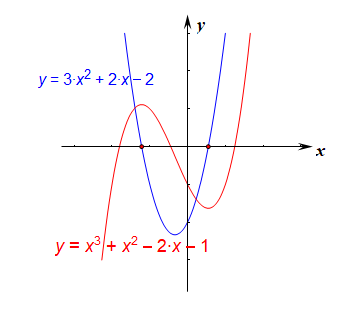
2、若$\Delta > 0$，令$y=F'(x)$的两个零点分别$m、n$，

则$F(x)$在区间$(-∞，m]$单增，在区间$[m,n]$单减，在区间$[n,+∞)$单增，

此时函数$F(x)$有极大值$F(m)$，有极小值$F(n)$，

我们结合导函数图像，可以作出原函数的草图，

$\fbox{例1}$【2014高考新课标Ⅰ卷理科，第11题】已知函数$f(x)=ax^3-3x^2+1$，若函数$f(x)$存在唯一零点 $x_0$，且$x_0>0$，则$a$的取值范围是【C】

$A(2，+\infty)$ $B(1，+\infty)$ $C(-\infty，-2)$ $D(-\infty，-1)$

法1：由于函数$f(x)$存在唯一零点 $x_0$，且$x_0>0$，

则方程$f(x)=0$有唯一的正实数解，即$ax^3-3x^2+1=0$有唯一的正实数解，

即方程$a=\cfrac{3x^2-1}{x^3}$有唯一的正实数解，

即函数$y=a$和函数$y=h(x)=\cfrac{3x^2-1}{x^3}=\cfrac{3}{x}-\cfrac{1}{x^3}(x>0)$有唯一的交点，

其余思路待补充。

法2：先将题目转化为，方程$ax^3=3x^2-1$有唯一的正实数解，

则静态函数$y=3x^2-1$和动态函数$y=ax^3$只能在区间$(0 ，+\infty)$上有交点，

此处需要我们知道函数$y=ax^3$的参变数$a$的作用，

由图像可知，当$a\leq 0$时，都不满足题意，故需要$a<0$，

但当$a$取很小的负值时，显然满足题意，当$a$为某一个恰当的负值时，两个曲线在$x<0$时可能相切，

当然，此处你可能还会认为是有相切，还有相交，这不要紧，我们通过下述的计算就能回答这个疑惑。

设切点坐标为$P(x_0，y_0)$，则有$x_0<0$，

则有$\left\{\begin{array}{l}{3ax_0^2=6x_0}\\{y_0=ax_0^3}\\{y_0=3x_0^2-1}\end{array}\right.$

解得$x_0=-1$，$y_0=2$，将切点$P(-1，2)$代入$y=ax^3$，解得$a=-2$，

故当$a<-2$时，两条曲线在$x<0$上没有交点，只在$x>0$上有交点，故满足题意，

即$a$的取值范围时$(-\infty，-2)$，故选$C$。

法3：利用导数方法，同时注意题目的隐含条件，$f(0)=1$，

$f'(x)=3ax^2-6x=3x(ax-2)$，

①当$a=0$时，原函数为$y=-3x^2+1$，有两个零点，不符合题意，舍去。

②当$a>0$时，由导函数的图像可知，函数$f(x)$在区间$(-\infty，0)$上单调递增，在区间$(0，\cfrac{2}{a})$上单调递减，在区间$(\cfrac{2}{a}，+\infty)$上单调递增，

此时函数在区间$(-\infty，0)$上必有一个零点，不符合题意，舍去。

③当$a<0$时，由导函数的图像可知，函数$f(x)$在区间$(-\infty，\cfrac{2}{a})$上单调递减，在区间$(\cfrac{2}{a}，0)$上单调递增，在区间$(0，+\infty)$上单调递减，

此时只需要函数$f(x)$的极小值大于零即可，即$f(\cfrac{2}{a})>0$，

即$a\cdot (\cfrac{2}{a})^3-3\cdot (\cfrac{2}{a})^2+1>0$，化简得到$a^2>4$，

解得$a<-2$或$a>2$，又$a<0$，故$a<-2$。

即$a$的取值范围时$(-\infty，-2)$，故选$C$。

转载于:https://www.cnblogs.com/wanghai0666/p/5906951.html

你可能感兴趣的文章